直积、直和、笛卡尔积、张量积的区别是什么

小朋友们好，今天我们来学习什么是笛卡尔积。我们把世界上所有上衣的集合叫做 $a$ ，世界上所有下着的集合叫做 $b$ ，那么 $a$ 和 $b$ 的笛卡尔积 $a \times b$ 是什么呢？就是所有可能的上下衣装搭配的集合啦（当然，不包括帽子、鞋子、首饰等等）。

现在我们打算开一家上衣店，专门卖上衣，叫做 $A$ 店；再开一家下着店，专门卖下着，叫做 $B$ 店。我们可以以一定数量进货各种各样的上衣，放到 $A$ 店里，再以一定数量进货各种各样的下着，放到 $B$ 店里。 $A$ 店的库存可以用一组整数来表示： $(a_1,a_2,\cdots,a_m),a_i\in \mathbb{Z}$ ， $B$ 店的库存也可以用一组整数来表示：$(b_1,b_2,\cdots,b_n),b_i\in \mathbb{Z}$ ，这些数字分别代表不同款型的数量。

所有可能的上衣店的集合构成一个环上的模（module over a ring），环的意思是上衣的数量只能是整数，而整数构成一个环，叫做整数环；模的意思就是我们可以把两个上衣店相加，得到一个新的上衣店，这个新店里的上衣就是把原来两个店的上衣给加起来。当然，我们也可以把两个上衣店相减，如果上衣的数量为负数，那么我们就说这个上衣店欠了市场多少件上衣。我们还可以将一家上衣店乘以一个整数得到一家新店，这个新店的库存是原店的整数倍。

如果两家店的库存完全相同，那么我们就说它们是同一家店，这是因为我们研究的实际上是抽象的库存，但是为了方便起见，我们就用店本身来代替库存啦。

以上所说的对下着店也成立，所有可能的下着店的集合也构成一个环上的模。

单卖上衣或者下着还是不得劲，于是我们直接把 $A$ 店与 $B$ 店合并起来。 $A$ 店与 $B$ 店的直和/直积就是这个新店啦。此时，我们可以用一组整数来表示它的库存： $(a_1,a_2,\cdots,a_m,b_1,b_2,\cdots,b_n)$ 。

张量积是什么呢？现在我们开一个套装店，只进货并且售卖上下衣的套装，不单卖上衣或者下着。那么此时所有这样的套装店的集合就是 $A$ 和 $B$ 的张量积 $A \otimes B$ 啦。这个新店的库存需要用一个表格来表示：

$\begin{pmatrix} c_{11} & c_{12} & \cdots & c_{1n} \\ c_{21} & c_{22} & \cdots & c_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ c_{m1} & c_{m2} & \cdots & c_{mn} \end{pmatrix}$

其中 $c_{ij}$ 表示由第 $i$ 款上衣与第 $j$ 款下着所构成的套装的数量。

OK，小朋友们，今天的代数课到此结束，回家记得好好完成课后阅读哦 ~ 下课 ~

（课后阅读）

如果现在我们开一家食品店，把上衣换成素菜、下衣换成荤菜，并且以千克来计重，那么此时的库存就可以用实数而不是整数来表示了，于是环上的模就升级成为了（域上的）向量空间，因为实数集不仅是一个环，还是一个域喔。

记所有素菜店的集合为 $A$ ，所有荤菜店的集合为 $B$ ，那么所有只售卖一荤一素套餐的店的集合就是 $A$ 与 $B$ 的张量积 $A \otimes B$ 啦。

思考题 1：售卖两荤一素套餐的店的集合是什么？
答案：并非 $A \otimes B \otimes B$ 。这是因为我们不能区分两个荤菜分别来自哪两个荤菜店。正确的答案是 $A \otimes (B\odot B)$ ，其中 $\odot$ 叫做对称积（symmetric product）。

思考题 2：如果两种荤菜必须不一样，那么这样的店的集合是什么？
答案： $A \otimes (B\wedge B)$ ，其中 $\wedge$ 叫做外积（exterior product）或者楔积（wedge product）。

以下是正经科普：

笛卡尔积

笛卡尔积是对集合做的。两个集合 $A$ 和 $B$ 的笛卡尔积定义为 $A\times B:={(a,b) \mid a\in A \wedge b\in B}$ 。就这么简单（只要你不研究它在集合论中的严格定义就行，严格的定义是由幂集公理给出的）。

直积

直积与笛卡尔积相同，除了有一点不同：直积可以携带集合上额外的结构（同态/态射），而笛卡尔积仅仅是对于集合本身而言的。

例如对于两个群 $A $ 和 $B$ 而言，其直积为 $A \times B$ ，且群运算定义为 $(a_1,b_1) \cdot (a_2, b_2) := (a_1 \cdot a_2, b_1 \cdot b_2)$ ，其中 $a_1,a_2 \in A, b_1,b_2\in B$ 。

对于两个向量空间 $A $ 和 $B$ 而言，由于向量空间只不过就是配备了数乘的阿贝尔群，且群运算为向量加法，因此直积在向量空间上的定义和在群上的定义相同：

$(a_1,b_1) +(a_2,b_2) :=(a_1 + a_2, b_1 + b_2)$

我们不能谈论两个集合之间的直积，因为集合上面没有像群的二元运算这样的额外结构。当一个人谈论直积的时候，谈论的对象一定不仅仅是集合，而是包含对应的运算。

直和

直和与直积在大多数情况下完全相同。不同之处非常微妙，涉及范畴学。一言以蔽之，直积属于 product，直和属于 coproduct。对于无穷次直积与直和，前者允许无穷多个不为单位元的元素，后者只允许有穷多个不为单位元的元素。见下一节。

直积与直和的泛性质

下图是直积与直和的泛性质的一个简单示意图。为了易懂，之后用群（group）代替范畴学中的对象（object），用同态（homomorphism）代替范畴学中的态射（morphism）。读者只要知道群和同态是什么，就能看懂。

这个图已经很清楚明白了，下面是具体的文字说明。

直积的泛性质如下：

对于任意两个群同态 $f_1:B \rightarrow A_1$ 和 $f_2: B\rightarrow A_2$ ，总是存在一个（在同构上意义唯一的）群 $A_1 \times A_2$ 以及同态 $\varphi:B\rightarrow A_1\times A_2$ ，使得 $f_i= \varphi \circ \pi_i (i=1,2)$ ，其中 $\pi_i$ 为投影映射（projection map），定义为 $\pi_1(a_1,a_2) := a_1,\pi_2(a_1,a_2):=a_2$ 。

$A_1$ 和 $A_2$ 的直积就是群 $A_1 \times A_2$ 和配备的投影映射 $\pi_{1,2}$ 。

注意，此处的 $\times$ 表示直积，而不是笛卡尔积。符号 $\times$ 既可以表示前者也可以表示后者，需要根据上下文确定。

直和的泛性质如下：

对于任意两个群同态 $g_1: A_1 \rightarrow B$ 和 $g_2: A_2 \rightarrow B$ ，总是存在一个（同构意义上）唯一的群 $A_1 \oplus A_2$ 以及同态 $\phi:A_1 \oplus A_2 \rightarrow B$ ，使得 $g_i=\iota_i \circ \phi (i=1,2)$ 。其中 $\iota_i$ 为包含映射（inclusion map），定义为 $\iota_1(a):=(a,e_{A_2}),\iota_2(a):=(e_{A_1},a)$ ，其中 $e_{A_i}$ 表示群 $A_i$ 的单位元。

$A_1$ 和 $A_2$ 的直和就是群 $A_1 \oplus A_2$ 和配备的包含映射 $\iota_{1,2}$ 。

可以看出来，直积与直和的同态方向是相反的。这也是 coproduct 中 co- 的来源，类似于 vector 和 covector。

直积与直和的不同

直积与直和的泛性质不同，这带来什么后果？

第一，有限多个对象的直积与直和是完全一样的，此时混用两者不会有问题。例如， $V \times W$ 同构于 $V\oplus W$ 。

第二，无穷多个对象的直积 $\times_{i=1}^{\infty} A_i$ 与直和 $\bigoplus_{i=1}^{\infty} A_i$ 是不一样的。后者只允许有限个元素不为单位元。这是因为群运算在定义上就是有穷的（如果想做无穷次群运算，通常需要借助极限等额外的概念），而直和的定义中会涉及无穷多次群运算。

具体来说，如果 $\bigoplus_{i=1}^{\infty} A_i$ 中存在一个有无穷多个元素不为单位元的元素 $a=(a_1,a_2,\cdots)$ ，那么它在同态 $\phi$ 下的像就是一个涉及无穷次群运算的东西 $\varphi(a)=g_1(a_1) \cdot g_2(a_2)\cdot \cdots$ ，这是不良定义的，因此也就不会存在这样一个同态 $\phi$ 。所以直和中不能包含有无穷多非单位元的元素。

直积与直和不同的一个例子

下面给出一个直和与直积不同的例子。我们考虑无穷个 $Z_2$ 的直和：

$\bigoplus _{i=1}^{\infty} Z_2 $

其中 $Z_2 = {0,1}$ 是二阶循环群。

它只包含有穷个元素不为零的元素，例如 $(1,0,1,0,0,\cdots)$ 。

而无穷个 $Z_2$ 的直积:

$\times_{i=1}^{\infty} Z_2$

它允许无穷个元素不为零，例如 $(1,0,1,1,1,\cdots)$ 。

前者与自然数集等势，因为它构成了自然数的二进制表示。

而后者与实数集等势，因为它构成了区间 $[0,1]$ 的二进制表示。

可见，前者可数而后者不可数，所以无穷个 $Z_2$ 的直和与无穷个 $Z_2$ 的直积是不同的。

张量积

直积与直和的定义只涉及到群，而张量积的定义通常涉及到向量空间（或者环上的模）。

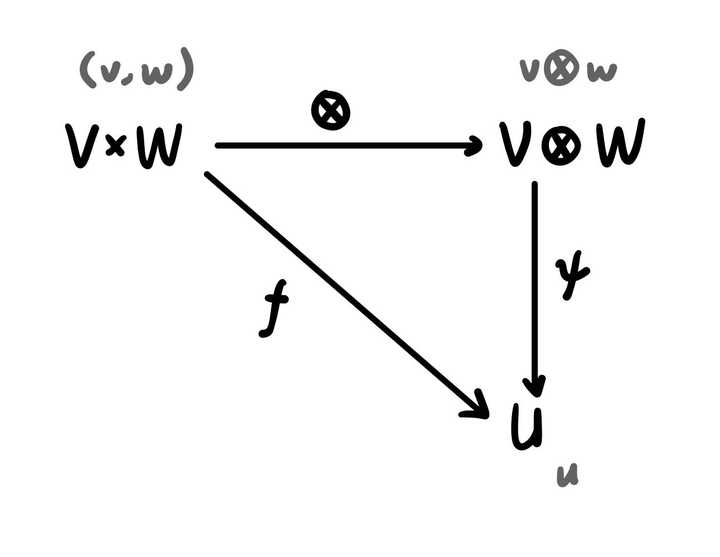
张量积的泛性质如下：

对于任意一个多重线性映射 $f:V\times W \rightarrow U$ ，都存在（同构意义上）唯一的向量空间 $V\otimes W$ ，以及映射 $\otimes:V\times W \rightarrow V \otimes W$ 和线性映射 $\psi: V \otimes W \rightarrow U$ ，使得 $f = \otimes \circ \psi$ 。这个向量空间 $V\otimes W$ 定义为 $V$ 和 $W$ 的张量积。此处符号 $\times$ 指笛卡尔积。

补充说明：多重线性映射是指有多个向量变量且对每个变量都是线性的映射。 具体来说， $n$ 重线性映射定义为 $f:V_1\times V_2\times \cdots\times V_n \rightarrow W$ ，且满足如下性质：
$\begin{align} &f(v_1,\cdots,\lambda a+ \mu b,\cdots,v_n)\\ &=\lambda f(v_1,\cdots,a,\cdots,v_n)+\mu f(v_1,\cdots,b,\cdots,v_n) \end{align}$

注意，在上述定义中，符号 $\otimes$ 有两个不同的意思，其一是向量空间之间的张量积 $V \otimes W$ ，其二是两个向量空间的元素做张量积运算，也就是从 $V\times W$ 到 $V \otimes W$ 的映射。

张量积与直积有什么不同？下面举例说明。假设 3 维向量空间 $V$ 有三个基： ${v_1,v_2,v_3}$ ，2 维向量空间 $W$ 有两个基： ${w_1,w_2}$ ，那么它们的直积 $V\times W$ 有五个基： ${(v_1,0),(v_2,0),(v_3,0),(0,w_1),(0,w_2)}$。 而 $V$ 和 $W$ 的张量积 $V \otimes W$ 有六个基： ${v_1\otimes w_1, v_1 \otimes w_2, v_2 \otimes w_1, v_2 \otimes w_2, v_3 \otimes w_1, v_3 \otimes w_2}$ 。

可以看出，直积的维数是 m + n，而张量积的维数是 m × n。

在中文（评论指正：包括英文）教材和互联网上，有很多人用直积来指张量积，这是错误的，但已经积重难返。当一个物理人对你说直积的时候，你要根据上下文判断他说的究竟是直积还是张量积。

当然，对于我们搞量子信息的物理人来说，当然是不会搞混的（骄傲），因为天天要用到张量积。复合系统的希尔伯特空间就是各个子系统的希尔伯特空间的张量积，这实际上是量子力学的公理之一。正因为是张量积而不是直积，才会出现量子纠缠。如果是直积的话，是不会有量子纠缠的。

太长不看版本

如果你越划越快，划到了这里，说明你不想看上面一大堆废话。OK，那么我给出简单的总结：

笛卡尔积、直积、直和基本上是一回事。不同之处在于：

1. 笛卡尔积是对集合所做的、直积与直和是对群（或者范畴学中的其他对象）所做的，并且把相应的群同态（范畴学中的态射）也给定义了一遍。
2. 直积与直和在做有限次的情况下没有区别。区别在于无穷次直积允许包含无穷多非单位元的元素，而无穷次直和只允许包含有限个非单位元的元素。

张量积与以上三者都有很大的不同，它一般是对向量空间（或者环上的模）定义的。直观地来看，m 维向量空间和 n 维向量空间的直和/直积的维数是 m + n，而张量积的维数是 m × n。