电磁场不只是电场和磁场——AB效应与Berry联络【更高更妙的电动力学·3】
电磁场并非电场和磁场。
换句话说,电磁场并不只是电场和磁场。
此话怎讲?
一、电磁势的地位高于场强
在前文中,我们挖过一个坑:
$\boxed{\begin{aligned} \phi &\mapsto \phi - \partial_t \lambda \\ \mathbf{A} &\mapsto \mathbf{A} + \nabla \lambda \end{aligned}}$
学过经典电动力学的同学都知道,这就是电磁规范变换,变换前后不影响实际的物理。
在经典电动力学中,我们总是把麦克斯韦方程当作第一性原理,而把规范变换看做是一种衍生品;我们把电场和磁场看做是根本性的实体,而将势能和矢势看做是一种方便的数学手段,认为它们没有实际的物理效应。而正是因为规范变换不影响电场和磁场,我们才导出了规范变换。
但,难道场强真的就是事实的全部吗?
不是的!从更高的视角来看,电磁势 $A = (\phi, \mathbf{A})$ 才是根本的物理实体,而场强是衍生品。
你可能有很多问题:在电动力学里,难道场强 $\mathbf{E}$ 和 $\mathbf{B}$ 不就是电磁场的全部吗?麦克斯韦方程不就是描述场强的变化吗?难道可观测量不是只有场强吗?由于规范自由度的存在,电磁势 $A = (\phi, \mathbf{A})$ 难道不是不可观测的吗?
的确,在经典电动力学里,以上的观点是完全正确的。
然而,当进入量子的领域之后,人们才逐渐发现,场强 $\mathbf{E}$ 和 $\mathbf{B}$ 并非事实的全部:有一些现象,只用 $\mathbf{E}$ 和 $\mathbf{B}$ 是无法解释的,只有用电磁势 $A$ 才能解释。
这个现象就是 Aharonov–Bohm 效应(简称 AB 效应)。直到 AB 效应的发现,人们才正式确立了 $A$ 的本体地位,而将场强 $\mathbf{E}$ 和 $\mathbf{B}$ 看成是衍生品。
在量子电动力学中,你几乎看不到 $\mathbf{E}$ 和 $\mathbf{B}$ 的身影。取而代之的是电磁势 $A$ 。
二、Aharonov-Bohm 效应
下面我们来简单推导一下 AB 效应。
在前文中我们讲到协变导数为 $D_\mu=\partial_\mu + \mathrm{i}\frac{e}{h}A_\mu$ 。
现在,我们让电子沿着某路径缓慢移动,那么其协变导数应当为零:
$D_\mu \psi = 0$
这正如在广义相对论中,我们让向量做平行移动时,要令其协变导数为零。
于是
$\begin{aligned} &D_\mu\psi=0\\ &\Rightarrow\left(\partial_\mu + \mathrm{i}\frac{e}{h}A_\mu\right) \psi =0 \\ &\Rightarrow \partial_\mu \psi = -\mathrm{i}\frac{e}{\hbar} A_\mu \psi \\ &\Rightarrow \psi(x) = \psi(x_0) \exp\left( -\mathrm{i}\frac{e}{\hbar}\int A_\mu \mathrm{d}x^\mu\right) \end{aligned}$
可见,除了动力学相位 $\int\frac{e}{\hbar}A_0 \mathrm{d}x^0 = \int\frac{1}{\hbar} E \mathrm{d}t$ 以外,电子还会增加一个额外的相位 $\color{red}{\int \frac{e}{\hbar} \mathbf{A} \cdot \mathrm{d}\mathbf{l}}$ 。这就是 Aharonov-Bohm 相位。
考虑一个很长的螺线管,其内部有磁场,但外部磁场为零。现在让电子缓慢绕其一周,相比螺线管未通电时,电子积累的相位变化了
$\boxed{\begin{aligned} \Delta \theta = \frac{e}{\hbar}\oint \mathbf{A} \cdot \mathrm{d}\mathbf{l} = \frac{e}{\hbar}\int \mathbf{B} \cdot \mathrm{d}\mathbf{S} = \frac{e }{\hbar}\Phi \end{aligned}}$
其中 $\Phi$ 是螺线管中的磁通量。
人们震惊地发现:电子没有经过任何 $\mathbf{E},\mathbf{B}$ ,换句话说,在电子的路径上, $\mathbf{E}=\mathbf{B}=\mathbf{0}$ ,但电子却仍然受到了电磁场的影响!这是因为在电子的路径上,虽然有 $\mathbf{E}=\mathbf{B}=\mathbf{0}$ ,但电磁矢势 $\mathbf{A}\ne 0$ 。
这告诉我们, $\mathbf{A}$ 才是根本的实体,而 $\mathbf{E}$ 和 $\mathbf{B}$ 只不过是衍生品而已。
的确,在前文中我们提到, $A$ 作为主丛上的联络,是第一性的。 $\mathbf{E}$ 和 $\mathbf{B}$ (或电磁张量 $F = \mathrm{d}A$ )作为联络 $A$ 的曲率,是第二性的。
注意, $\Delta \theta = \frac{e}{\hbar}\oint \mathbf{A} \cdot \mathrm{d}\mathbf{l}$ 是规范不变的:令 $\mathbf{A} \rightarrow \mathbf{A} + \nabla\lambda$ ,有 $\oint \nabla \lambda\cdot \mathrm{d}\mathbf{l} = 0$ 。可见,只有闭合路径的 AB 相位才是规范不变的。
三、和乐(Holonomy)
在纤维丛的底流形上绕一圈回到原点,导致纤维中的值发生改变,这个现象叫做和乐(Holonomy)。对于我们的 $U(1)$ 主丛,其纤维是 $U(1)$ ,此时是 $U(1)$ 中的元素( $\mathrm{e}^{\mathrm{i}\theta}$ )发生了变化。
这正如一个切向量在球面上绕一圈回到原点之后,该切向量会发生变化,因为切向量就是切丛的纤维(切空间)中的元素。
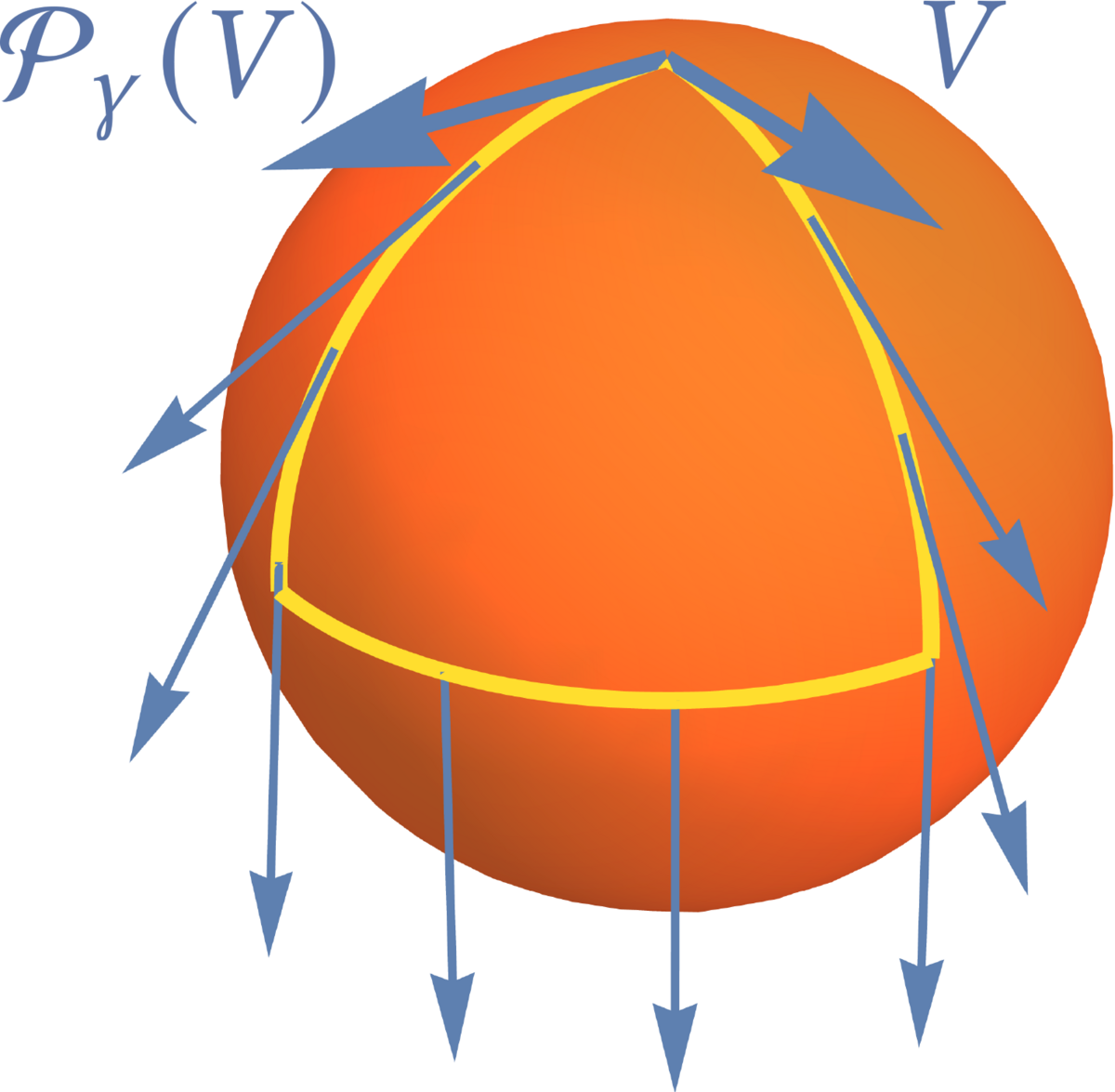
切丛上的 Holonomy
在物理学中,$U(1)$ 纤维丛上的 Holonomy 有个特别的名字,叫做几何相位(Geometric Phase),或者 Berry 相位。其对应的联络叫做 Berry 联络,对应的曲率叫做 Berry 曲率。
在 AB 效应中,Berry 联络 $\mathcal{A}$ 不是别的,正是电磁 1-形式 $A$ (实际上还要乘以常数 $e/\hbar$ : $\mathcal{A} = \frac{e}{\hbar} A$ ),而 Berry 曲率 $F$ 就是磁场 $B$ (实际上还要乘以常数 $e/\hbar$ : $F = \frac{e}{\hbar} B$ )。
更准确地说,Berry 曲率应当是 $A$ 的外微分 $F = \mathrm{d}A$ ,是一个 2-形式。
通过三维欧式空间的 Hodge 对偶,我们可以将 2-形式对偶成一个 1-形式,也就是磁场 1-形式。对 1-形式 $A$ 求外微分再求 Hodge 对偶等价于求它的旋度: $\nabla \times A^\sharp = \star\mathrm{d}A$ 。
之所以人们把磁场叫做赝矢量,也是因为磁场本质上是一个 2-形式,而非一个 1-形式。我们常说的磁场其实是这个 2-形式的 Hodge 对偶。
电磁势 $\mathbf{A}$ 只是一个特定的 $U(1)$ 纤维丛上的联络,这个纤维丛的底流形是位形空间自身。
还有其他更多的 $U(1)$ 纤维丛,它们的底流形不是位形空间,而是抽象的参数空间,比如动量空间。对量子霍尔效应的分析就是在动量空间的 $U(1)$ 纤维丛上进行的,在那里我们同样可以导出 Berry 联络和 Berry 曲率,这些概念成为了现代凝聚态物理的核心。
$U(1)$ 纤维丛上的几何相位叫做 Berry 相位, $SU(n)$ 纤维丛上的几何相位叫做非阿贝尔几何相位,在非厄米系统、拓扑量子计算等中都有应用。
四、Berry 联络/曲率
接下来我们来推导 Berry 联络的公式。
现在考虑一个抽象的底流形 $M$ , $M$ 上的点 $s \in M$ 是哈密顿量 $H(s)$ 的参数,而不是时空点。此时记哈密顿量的某个本征态为 $\psi$ 。
从平行移动出发:
$\begin{aligned} &D_\mu\psi=0\\ &\Rightarrow\left(\partial_\mu + \mathrm{i}A_\mu\right) \psi =0 \\ &\Rightarrow \partial_\mu \psi = -\mathrm{i}A_\mu \psi \end{aligned}$
上式两边与 $\psi$ 求内积,得到:
$\langle\psi | \partial_\mu \psi \rangle = -\mathrm{i} A_\mu \langle\psi | \psi\rangle$
即:
$\boxed{A_\mu = \mathrm{i} \langle \psi | \partial_\mu \psi\rangle}$
这就是 Berry 联络的表达式。也可以写成:
$\boxed{\mathbf{A} = \mathrm{i} \langle \psi|\nabla \psi\rangle}$
而 Berry 曲率为 Berry 联络的外微分:
$F = \mathrm{d}A$
写成指标形式则为
$ \begin{aligned} F_{\mu\nu} &= \partial_\mu A_\nu - \partial_\nu A_\mu \\ &= \mathrm{i} \left[\partial_\mu \langle \psi | \partial_\nu \psi\rangle -\partial_\nu \langle \psi | \partial_\mu \psi\rangle \right] \\ &= \mathrm{i} [\langle \partial_\mu \psi| \partial_\nu \psi \rangle - \langle \partial_\nu \psi| \partial_\mu \psi \rangle] \end{aligned} $
即
$\boxed{F_{\mu\nu}=\mathrm{i} [\langle \partial_\mu \psi| \partial_\nu \psi \rangle - \langle \partial_\nu \psi| \partial_\mu \psi \rangle]}$
几何相是联络 1-形式 $A$ 在闭合曲线 $\gamma$ 上的积分:
$\boxed{ \Delta \theta = \int_\gamma A }$
如果存在曲面 $\Sigma$ 使得曲线 $\gamma$ 是 $\Sigma$ 的边界,那么根据 Stokes 定理,有
$\begin{aligned} \Delta \theta = \int_{\partial \Sigma} A = \int_{\Sigma} \mathrm{d}A = \int_\Sigma F \end{aligned}$
其中 $\partial \Sigma$ 表示 $\Sigma$ 的边界。
所以几何相也可以由曲率 2-形式 $F$ 在曲面 $\Sigma$ 上积分得到:
$\boxed{ \Delta \theta = \int_\Sigma F}$
如果我们取 $\Sigma$ 为闭合曲面,则有 $\partial \Sigma=0$ ,此时有
$\Delta \theta = \int_\Sigma F = \int_{\partial \Sigma} A = 0$
然而,在非拓扑平凡的流形上,这个积分不一定为零。这是因为此时无法定义全局的联络 $A$ ,导致 Stokes 定理不再适用。详情我们在下一篇文章中介绍。
注意,几何相 $\Delta \theta$ 并非 $U(1)$ 中的元素,而是 $U(1)$ 的李代数中的元素。换句话说,几何相并不是在 $U(1) = { e^{\mathrm{i}\theta} \mid \theta \in [0,2\pi) }$ 上取值,而是在 $\mathbb{R}$ 上取值。它代表相位的变化量,而不是相位本身。也就是说,几何相可以取 $2\pi, 4\pi$ 等等,且它们和 $0$ 不等价。
在二维晶格中,由于周期性边界条件的存在,电子的动量空间 $M$ 是一个 Torus,即 $M=T^2$ 。此时在 $T^2$ 上对 Berry 曲率 $F$ 积分,就能得到陈数,它不一定为零:
$\int_{M} F = 2 k\pi \quad (k\in\mathbb{Z})$
其中 $k$ 就是陈数,定义为 $k = \frac{1}{2\pi}\int_{M} F$ 。