规范场论视角下的电动力学【更高更妙的电动力学·2】
这篇文章需要用到很多上一篇文章中的概念,因此请确保你阅读了上一篇文章。
本文依然采用 $(-,+,+,+)$ 的度规约定。
为什么说电动力学是规范场论?
为了搞清楚这句话是什么意思,我们需要先弄清楚什么是电动力学,以及什么是规范场论。
前者我相信大部分读者都已经学过,而后者才是本篇文章要强调的内容。
让我们开始吧!
一、什么是规范变换(经典电动力学)
首先,什么叫规范场论?规范场论就是拉氏量(或者更广义地说,物理理论本身)在局域变换下不变的理论。
那么,什么是局域变换?
对于电磁场来说,局域变换就是 $\boxed{ A_\mu \mapsto A_\mu + \partial_\mu \lambda }$ ,这是协变形式。而逆变形式才是我们通常所说的向量: $A^\mu = g^{\mu\nu}A_\nu$ ,即 $A^\mu = (-A_0,A_1,A_2,A_3)$ 。因此 $A_\mu \mapsto A_\mu + \partial_\mu \lambda $ 等价于:
$\boxed{ \begin{aligned} \phi &\mapsto \phi - \partial_t \lambda \\ \mathbf{A} &\mapsto \mathbf{A} + \nabla \lambda \end{aligned} }$
学过经典电动力学的同学都知道,这就是电磁规范变换,变换前后不影响实际的物理。规范变换是一个局域变换,这是因为 $\lambda$ 并非一个常数,而是时空点的函数。
在经典电动力学中,我们总是把麦克斯韦方程当作第一性原理,而把规范变换看做是一种衍生品;我们把电场和磁场看做是根本性的实体,而将势能和矢势看做是一种方便的数学手段,认为它们没有实际的物理效应。而正是因为规范变换不影响电场和磁场,我们才导出了规范变换。
但,难道场强真的就是事实的全部吗?
不是的!从更高的视角来看,势能和矢势(4-势)才是根本的物理实体,而场强是衍生品。
这是有物理证据的: Aharonov–Bohm 效应(简称 AB 效应)告诉我们,势能和矢势(4-势)有实实在在的物理影响。而规范变换也不只是一种数学技巧,而是具有一定的本体性地位。
此般种种,其背后的原因要到量子电动力学中去寻找答案。
二、什么是规范变换(量子电动力学)
相信很多同学都听说过,标准模型的规范群是 $U(1) \times SU(2) \times SU(3)$ 。其中 $U(1)$ 对应光子(电磁场), $SU(2)$ 对应弱玻色子(W 和 Z 玻色子), $SU(3)$ 对应胶子。
实际上,在量子电动力学中,规范变换指的是局域的 $U(1)$ 变换,也就是形如 $\psi(x) \mapsto e^{\mathrm{i}\theta(x)} \psi(x)$ 的变换,这里 $\psi$ 指的是电子的波函数,它是一个狄拉克场。
局域变换与全局变换的不同之处在于,局域变换中的 $\theta$ 本身也是一个场,而全局变换的 $\theta$ 是一个常数。
顺便提一句,根据诺特定理,全局的 $U(1)$ 对称性可以导出电荷守恒。不过这不是本篇关心的内容。
如果我们要求理论满足局域对称性,即物理在局域变换 $\psi \mapsto e^{\mathrm{i}\theta}\psi$ 下保持不变,那么就会导致电磁场的出现。换句话说,每一个局域规范对称性都会对应一个规范场。
此话从何说起呢?
我们先来看局域变换 $\psi \mapsto e^{\mathrm{i}\theta}\psi$ 会导致什么。由于我们还没有规定拉氏量,所以我们只能考察与 $\psi$ 自身有关的量。比如 $\partial_\mu \psi$ 。
我们希望在局域变换 $\psi \mapsto e^{\mathrm{i}\theta}\psi$ 下, $\partial_\mu\psi$ 也按照同样的方式变换,即 $\partial_\mu\psi \mapsto e^{\mathrm{i}\theta}\partial_\mu\psi$ 。
为什么我们要求 $\partial_\mu\psi$ 的变换方式与 $\psi$ 相同?
这一点可以从狄拉克场的拉氏量得出。为了保持狄拉克场的拉氏量 $\mathcal{L}=\bar{\psi}(\mathrm{i}\hbar c \gamma^\mu \partial_\mu \psi -mc^2)\psi $ 不变,我们要求 $\partial_\mu\psi$ 的变换方式应当与 $\psi$ 相同。
这一点也可以从狄拉克方程 $\mathrm{i}\hbar \gamma^\mu (\partial_\mu \psi) -mc,\psi =0$ 中看出。实际上,狄拉克方程就是通过对狄拉克场的作用量变分得到的。
如果我们把 $\psi \mapsto e^{\mathrm{i}\theta}\psi$ 代入 $\partial_\mu\psi$ :
$\begin{aligned} \partial_\mu \psi \mapsto \partial_\mu(e^{\mathrm{i}\theta} \psi) &= e^{\mathrm{i}\theta}\left[\partial_\mu \psi \color{red}{+ \mathrm{i}(\partial_\mu\theta) \psi}\right] \\ &= e^{\mathrm{i}\theta}\left[(\partial_\mu \color{red}{+ \mathrm{i}\partial_\mu\theta}) \psi\right] \end{aligned}$
就会发现,结果多了一项 $ \color{red}{\mathrm{i}(\partial_\mu\theta) \psi}$ ,因此我们需要想办法消去它。
我们不妨引入 $D_\mu = \partial_\mu - \mathrm{i} (\partial_\mu\theta)$ ,于是:
$\begin{aligned} D_\mu \psi \mapsto D_\mu(e^{\mathrm{i}\theta} \psi) &= \left[\partial_\mu \color{red}{- \mathrm{i} (\partial_\mu\theta)}\right] (e^{\mathrm{i}\theta} \psi) \\ &= e^{\mathrm{i}\theta}\partial_\mu \psi \end{aligned}$
额…好吧,有点尴尬,我们并没有实现 $D_\mu\psi \mapsto e^{\mathrm{i}\theta} D_\mu \psi$ ,而是实现了 $D_\mu\psi \mapsto e^{\mathrm{i}\theta} \partial_\mu \psi$ 。
怎么样才能实现 $D_\mu\psi \mapsto e^{\mathrm{i}\theta} D_\mu \psi$ 呢?
我们不妨让 $\color{red}{-(\partial_\mu\theta)}$ 这一项本身成为一个场 $A_\mu$ 。这是什么意思呢?意思我们就是要创建一个新的场 $A_\mu$ ,这个新的场的变换规则是 $A_\mu \mapsto A_\mu \color{red}{- (\partial_\mu\theta)}$ 。
接着,我们令 $\boxed{ D_\mu = \partial_\mu + \mathrm{i}A_\mu }$ 。
现在我们再试一次:
$\begin{aligned} D_\mu \psi \mapsto D_\mu^\prime(e^{\mathrm{i}\theta} \psi) &= \left[\partial_\mu + \mathrm{i} (A_\mu \color{red}{- \partial_\mu\theta})\right] (e^{\mathrm{i}\theta} \psi) \\ &= e^{\mathrm{i}\theta}\left(\partial_\mu + \color{red}{\cancel{\mathrm{i}\partial_\mu\theta}} + \mathrm{i}A_\mu - \color{red}{\cancel{\mathrm{i}\partial_\mu\theta}} \right) \psi \\ &= e^{\mathrm{i}\theta}D_\mu \psi \end{aligned}$
我们成功了!这样定义出来的 $D_\mu$ 叫做协变导数。
注意,这里的协变导数是主丛上的协变导数,与矢量丛上的协变导数 $\nabla_\mu$ 不是一回事。后者刻画的是矢量丛纤维(切空间)之间的联络,描述了流形本身的弯曲。而协变导数 $D_\mu$ 刻画的是主丛纤维之间的联络,描述的是流形内部自由度的弯曲。我们在第四节会详细展开。
诶,你有没有觉得 $\boxed{A_\mu \mapsto A_\mu \color{red}{- (\partial_\mu\theta)}}$ 这个玩意儿有点眼熟?它不就是第一节里说到的电磁规范变换吗?
或写成 $A \mapsto A - \mathrm{d}\theta$
其实这个新的场 $A_\mu$ 就是电磁场。正是它的存在保证了局域规范变换不会改变拉氏量。
为了兼容 SI 单位制,我们给 $A_\mu$ 乘以一个量纲常数: $D_\mu = \partial_\mu + \mathrm{i}\frac{e}{\hbar} A_\mu$ ,从而保证 $A_\mu$ 拥有正确的量纲。其中 $e$ 是元电荷,为正数。根据度规约定以及 $e$ 的符号的不同,也可能写成 $D_\mu = \partial_\mu - \mathrm{i}\frac{e}{\hbar} A_\mu$ 。
在经典电动力学中,之所以带电粒子的哈密顿量要把 $\mathbf{p}$ 换成 $(\mathbf{p} - e \mathbf{A})$ ,也和协变导数有关。下面给读者几个有趣但非常简单的练习:
将量子力学中的 $\hat{p}_\mu = -\mathrm{i}\hbar \partial_\mu$ 换成 $\hat{p}_\mu = -\mathrm{i}\hbar D_\mu$ ,得到正则动量 $\mathbf{p} = \mathbf{p}_{\text{kin}} + e\mathbf{A}$ ,其中 $\mathbf{p}_{\text{kin}} = m\dot{\mathbf{x}} = -\mathrm{i}\hbar \nabla$ 是运动动量(kinetic momentum)。
于是带电粒子的能量(哈密顿量)为:
$\begin{aligned} H(\mathbf{x},\mathbf{p})&=\frac{1}{2m}(\mathbf{p}_{\text{kin}})^2 + e\phi(\mathbf{x}) \\ &=\frac{1}{2m}[\mathbf{p} - e\mathbf{A}(\mathbf{x})]^2 + e\phi(\mathbf{x}) \end{aligned} $利用正则方程 $\dot{x}^\mu = \frac{\partial H}{\partial p_\mu}, \quad \dot{p}_\mu = -\frac{\partial H}{\partial x^\mu}$ 得到洛伦兹力: $\dot{\mathbf{p}}=e(\mathbf{E}+\dot{\mathbf{x}} \times \mathbf{B})$ 。注意此处粒子带正电荷 $+e$ 。对于电子,需要将 $+e$ 换成 $-e$ 。
给定带电粒子的拉氏量 $L(\mathbf{x}, \dot{\mathbf{x}}) = \frac{1}{2} m \dot{\mathbf{x}}^2 + e \dot{\mathbf{x}} \cdot \mathbf{A} - \phi(\mathbf{x})$ ,通过 $p_\mu := \frac{\partial L}{\partial \dot{x}_\mu}$ 得到正则动量 $\mathbf{p} = m\dot{\mathbf{x}} + e \mathbf{A}$ 。
利用欧拉-拉格朗日方程 $\frac{\partial L}{\partial x^\mu} - \frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial \dot{x}^\mu} = 0$ ,得到洛伦兹力: $\dot{\mathbf{p}}=e(\mathbf{E}+\dot{\mathbf{x}} \times \mathbf{B})$
通过勒让德变换 $H = \mathbf{p} \cdot \dot{\mathbf{x}} - L$ 得到哈密顿量,并与 2 中的哈密顿量比较。它们应当相同。
三、狄拉克场和电磁场的拉氏量
不太了解狄拉克方程的同学可以跳过本节。
现在,我们将 $D_\mu = \partial_\mu + \mathrm{i}\frac{e}{\hbar} A_\mu$ 代入狄拉克场的拉氏量 $\mathcal{L}=\bar{\psi}(\mathrm{i}\hbar c \gamma^\mu \partial_\mu -mc^2)\psi $ 得:
$\begin{aligned} \mathcal{L}_{\text{Dirac}}&=\bar{\psi}(\mathrm{i}\hbar c \gamma^\mu D_\mu-mc^2)\psi \\&=\bar{\psi}(\mathrm{i}\hbar c \gamma^\mu \partial_\mu -mc^2)\psi \color{red}{- eA_\mu c\bar{\psi} \gamma^\mu \psi} \end{aligned}$
令 $J^\mu = -ec\bar{\psi} \gamma^\mu \psi$ (注意,电流的方向与电子运动方向相反)得:
$\begin{aligned} \mathcal{L}_{\text{Dirac}}&=\bar{\psi}(\mathrm{i}\hbar c \gamma^\mu \partial_\mu-mc^2)\psi \color{red}{+ A_\mu J^\mu} \end{aligned}$
上式第二项正是上篇文章中的有源项:
$\begin{aligned} \mathcal{L}_{\text{EM}} = -\frac{1}{4\mu_0} F_{\mu\nu} F^{\mu\nu} \color{red}{+ A_{\mu} J^{\mu} } \end{aligned}$
因此,总的拉氏量为:
$\boxed{ \begin{aligned} &\mathcal{L}[A_\mu, \partial_\nu A_\mu;\psi,\partial_\mu \psi;\bar\psi,\partial_\mu\bar\psi] \\&= \bar{\psi}(\mathrm{i}\hbar c \gamma^\mu \partial_\mu -mc^2)\psi - eA_\mu c\bar{\psi} \gamma^\mu \psi -\frac{1}{4\mu_0} F_{\mu\nu} F^{\mu\nu} \end{aligned} }$
对作用量 $S=\int\mathcal{L} \mathrm{d}^4x$ 变分,就可以同时得到狄拉克方程和麦克斯韦方程。这就是量子电动力学的拉格朗日表述的基础。
四、主丛上的联络
实际上, $A_\mu$ 是主丛上的联络。这里的主丛指的是一个 $U(1)$ -纤维丛。
什么是主丛?可以把主丛想象成一个流形,这个流形上的每一个点都附带了一个“纤维”,且这个纤维拥有李群的结构。
李群的定义:如果一个流形本身也是一个群,那么这个流形就叫做李群。
主丛与向量丛的区别在于:向量丛的纤维是向量空间例如切空间/余切空间;而主丛的纤维是李群(严格来说,是李群的 torsor)。
对于电动力学而言,我们所考虑的主丛,其纤维是 $U(1)$ :你可以想象时空流形上的每一点都长出了一个圆圈。这些圆圈就是我们所说的纤维,它们代表着相位。
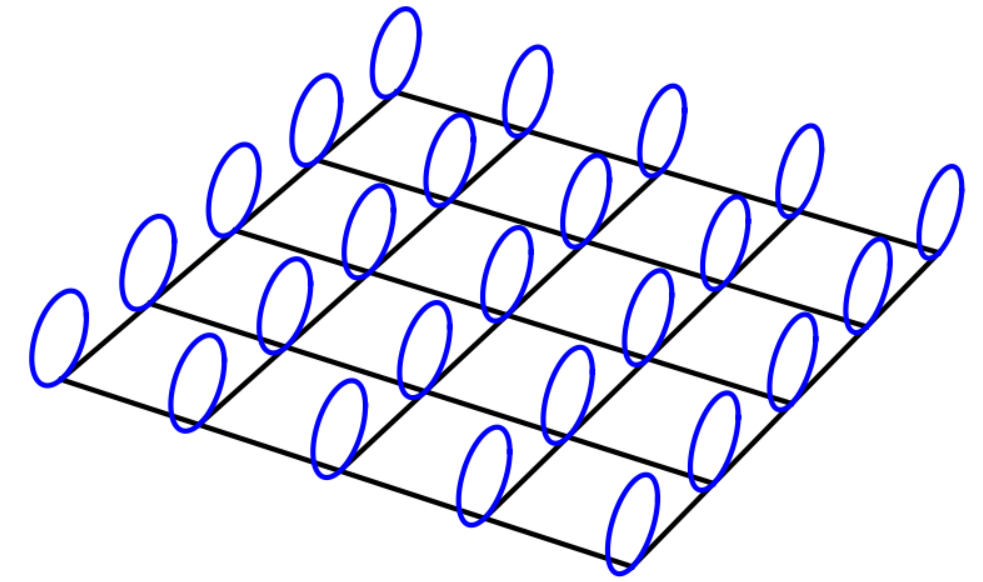
U(1) 纤维丛,图源:ChatGPT 作图
在上图中,这些圆圈被画在了分立的点上,这只是为了方便展示。实际上,每一个点上都有一个这样的圆圈。
纤维丛上的联络描述的就是纤维之间连接的方式。具体到我们的 $U(1)$ 主丛,就是上图中的圆圈之间连接的方式。
主丛上的联络 $A$ 定义为一个李代数取值的 1-形式。由于 $U(1)$ 的李代数很简单,就是 $\mathbb{R}$ ,所以看起来与普通的 1-形式没什么不同。
选读
李代数的定义:李代数是李群在单位元处的切空间,且该切空间额外附带了一个二元运算,即李括号 $[\cdot, \cdot]$ 。
以李群 $U(1)$ 为例,李群本身是 ${\mathrm{e}^{\mathrm{i}\theta} \mid \theta\in[0,2\pi)}$ ,而李代数是 $\mathrm{i}\mathbb{R} = {\mathrm{i} \theta\mid \theta \in \mathbb{R}}$ 。在物理中,我们通常把 $\mathrm{i}$ 去掉,而把 $\mathbb{R}$ 说成是李代数。
从 $A_\mu \mapsto A_\mu - (\partial_\mu\theta)$ 这个式子我们可以看出,作为 1-形式的 $\partial_\mu \theta$ 的取值应当是李代数中的元素。
李代数上的李括号是由李群上的左不变矢量场的李导数 $\mathcal{L}_V W=[V,W]$ 所诱导的。具体来说,单位元的切空间中的每一个元素都唯一对应李群上的一个左不变矢量场。通过左不变矢量场之间的李括号,我们就能反过来得到切空间上的李括号,从而使其成为一个李代数。
余切空间自然地拥有外代数结构,而切空间自然地拥有李代数结构。
曲率定义为联络的外微分: $F=\mathrm{d}A$ 。可以想象,上图中的圆圈并不是普通地粘在一起,而是以一种特定的,扭曲的方式粘在一起。联络的曲率所描述的,正是纤维之间这种弯曲的连接方式。从 $A$ 的变换规则可以看出这一点: $A_\mu \mapsto A_\mu \color{red}{- (\partial_\mu\theta)}$ ,它描述的就是相位在移动中的变化 $(\partial_\mu \theta)$ 。
令协变导数 $D_\mu \psi = \partial_\mu \psi +\mathrm{i}A_\mu \psi =0$ ,我们就能得到主丛上的平行移动:
$\begin{aligned} &D\psi=0\\ &\Rightarrow\left(\partial_\mu + \mathrm{i}\frac{e}{h}A\right) \psi =0 \\ &\Rightarrow \partial_\mu \psi = -\mathrm{i}\frac{e}{\hbar} A_\mu \psi \\ &\Rightarrow \psi(x) = \psi(x_0) \exp\left( -\mathrm{i}\frac{e}{\hbar}\int A_\mu \mathrm{d}x^\mu\right) \end{aligned}$
可见,除了动力学相位 $\int\frac{e}{\hbar}A_0 \mathrm{d}x^0 = \int\frac{1}{\hbar} E \mathrm{d}t$ 以外,平行移动还会增加一个额外的相位 ${\int \frac{e}{\hbar} \mathbf{A} \cdot \mathrm{d}\mathbf{l}}$。这就是几何相位。详情我们会在本系列以后的文章中介绍。
换句话说,电磁场的场强张量 $F$ 正是主丛纤维之间连接的曲率。这就是电磁场作为主丛上的联络的几何意义。
我们常说引力是几何效应。但从以上分析可见,电磁力(以及下文要介绍的弱力和强力)也未尝不是几何效应!只是前者对应向量丛上的联络,后者对应主丛上的联络。
五、杨-米尔斯(Yang-Mills)理论
有了以上这么多数学铺垫,我们完全可以介绍一下杨-米尔斯理论了。
我们在上一篇文章介绍的拉氏量:
$\boxed{ \begin{aligned} \mathcal{L} = -\frac{1}{2} F \wedge (\star F) + A\wedge (\star J) \end{aligned} }$
在杨-米尔斯理论中完全适用。只不过此时的 $A$ 不仅可以是 $U(1)$ -纤维丛上的联络,还可以是 $SU(2)$ 、 $SU(3)$ -纤维丛上的联络。它们的李代数分别写作 $\mathfrak{u}(1), \mathfrak{su}(2), \mathfrak{su}(3)$ 。
与 $\mathfrak{u}(1)$ 只有 1 个生成元不同, $\mathfrak{su}(2)$ 的生成元有 3 个, $\mathfrak{su}(3)$ 的生成元有 8 个,也就是说它们的维数分别是 3 和 8。此时有 $A_\mu = A_\mu^a T^a$ ,其中 $T^a$ 是李代数的生成元,可以作为李代数的一组基。
与 $U(1)$ 不同, $SU(2)$ 和 $SU(3)$ 是非交换群(非阿贝尔群),因此基于它们的规范场论也叫非阿贝尔规范场论。
由于非交换性,曲率不再是简单的 $F=\mathrm{d}A$ ,而是 $F=\mathrm{d}A+ A\wedge A$ ,其中 $\wedge$ 是微分形式的 wedge product。之所以 $A \wedge A \ne 0$ ,也是因为非交换性: $A \wedge A = A_\mu^a A_\nu^b (T^a T^b - T^b T^a) = A_\mu^a A_\nu^b [T^a, T^b]\ne 0 $ 。
每一个生成元都对应一个场,对应的粒子叫做规范玻色子。对于 $U(1)$ 而言,规范玻色子是光子,传递电磁力。对于 $SU(2)$ 而言,规范玻色子是 $W^\pm,Z^0$ ,它们传递弱力。对于 $SU(3)$ 而言,规范玻色子是 8 个胶子,它们传递强力。
实际上电磁力和弱力没有这么简单, $U(1)$ 对应的粒子原本是 $B$ , $SU(2)$ 对应 $W^1,W^2,W^3$ 。希格斯机制所导致的自发对称性破缺使得它们混合在了一起:
$\begin{aligned} W^\pm &= \frac{W^1 \pm \mathrm{i} W^2}{\sqrt{2}} \\ Z^0 &= W^3 \cos(\theta_W) - B \sin(\theta_W) \\ A &= W^3 \sin(\theta_W) + B\cos(\theta_W) \end{aligned}$
这才有了光子 $A$ 和弱玻色子 $W^\pm,Z^0$。具体机制由于篇幅所限就不介绍了。